Tính căn bậc hai của một số như thế nào?

Đới sống hàng ngày 6 Minutes

sr

Hôm nay mình mới đăng ký khóa học MITx: 6.00.1x Introduction to Computer Science and Programming Using Python trên edX và biết được thuật toán tìm căn bậc hai của một số khá là hay nên muốn chia sẻ cùng mọi người.
Thuật toán tìm căn bậc hai của một số. Nghe có vẻ hơi ngô nghê vì từ trước đến nay hầu hết chúng ta đều tìm căn bậc hai của một số bằng cách … ấn máy tính. Hay trước khi có máy tính, lúc chúng ta còn nhỏ (không được dùng máy tính) thì chúng ta học thuộc. Ví dụ như bình phương của 13 là 169 hay căn bậc hai của 289 là 17. Mình còn nhớ đứa bạn mình hồi cấp hai bị chép phạt 100 lần vì không thuộc bảng bình phương từ 1 đến 20 :)) Dường như việc tìm căn bậc hai dương của một số là một điều gì đó rất… bí ẩn và không rõ ràng. Chính vì thế nên bài viết này mình sẽ viết về thuật toán để thực hiện công việc đó. Một điều có lẽ nghe rất đơn giản nhưng … bị nhiều người bỏ quên 😀 Hi vọng nó có ích đối với mọi người.

Thuật toán và ví dụ

Thuật toán tìm căn bậc hai của một số

Giả sử ta đang cần tìm căn bậc hai của x

Bước 0: Chọn một số mà bạn “nghĩ” là căn bậc hai của x. Gọi nó là g

Bước 1: Tính g^2. Nếu x = g^2 thì g là số thỏa mãn. Bài toán được giải

Bước 2: Tính \frac{1}{2} (g + \frac{x}{g}) Gán nó vào g. Quay lại bước 1

Sau đây mình sẽ chạy thuật toán này trên một số ví dụ. Mình sẽ lấy một ví dụ đơn giản trước tiên.

Tìm căn bậc hai của 25

Mình sẽ lập một cái bảng để theo dõi thuật toán một cách trực quan hơn

Bước đầu tiên ta sẽ tìm một số mà ta “đoán” nó là căn bậc hai của 25. Dĩ nhiên chúng là ai cũng biết số-đó-là-số-nào-đấy. Nhưng mình giả sử mình không biết mà mình đoán “Căn bậc hai của 25 là g=3“.

Bước 1: Mình tính g^2 = 9 và kiểm tra nó chưa bằng x, nên chuyển sang bước 2

Bước 2: Tính \frac{1}{2}.(g+\frac{x}{g}) = 5.67 rồi gán lại cho g. Sau đó mình quay lại bước 1

Bước 1: Kiểm tra xem g^2 = x hay không. Ta có g^2 = 32.11 chưa thỏa mãn nên ta chuyển tới bước 2.

Bước 2: Tính \frac{1}{2}.(g+\frac{x}{g}) = 5.04. Theo thuật toán nêu trên chúng ta chuyển tới bước 1.

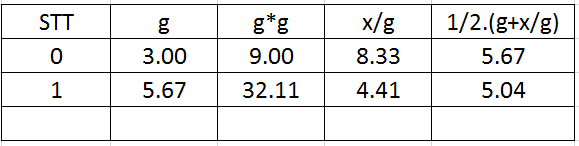
Bước 1: Tính g^2 = 25.39. Đến đây chúng ta có thể khá là “hài lòng” về kết quả mà ta thu được rồi. 5.04 là một kết quả khá là chính xác và chấp nhận được và có thể kết thúc thuật toán. Tuy nhiên nếu bạn là một người cầu toàn, chúng ta có thể tiếp tục chạy thuật toán thêm một vài lần nữa.

Bước 2: \frac{1}{2}.(g+\frac{x}{g}) = 5.00. Đến đây có lẽ thuật toán đã thuyết phục được tất cả các bạn rồi chứ? 😀

Chúng ta có thể thấy chỉ sau hai vòng lặp chúng ta đã có kết quả chính xác tới một chữ số thập phân căn bậc hai của 25 và thêm một vòng lặp nữa thì độ chính xác đã tăng lên rất nhiều. Các bạn thấy đó, đâu lúc nào cũng cần phải sự trợ giúp của máy tính và học thuộc lòng chúng ta mới tính được phép toán này đâu. Chỉ với một chút cộng trừ nhân chia đơn giản, công việc bí hiểm xưa nay vốn trở nên rõ ràng và quen thuộc vô cùng. Chúng ta hãy thử lấy thêm một vài ví dụ nữa nhé.

Chạy thuật toán với x = 170
Chạy thuật toán với x = 802
Chạy thuật toán với x = 2634
Chạy thuật toán với x = 1123172323

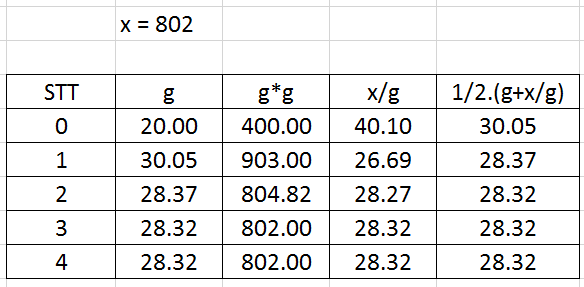
Wao, cảm giác thật dễ chịu khi nút căn bậc hai của chiếc máy tính không thể vênh mặt lên với chúng ta được nữa. Thậm chí với với số có 10 chữ số cũng chỉ mất 4 vòng lặp để tìm ra được kết quả chính xác đến hai số thập phân (Các bạn có thể kiểm tra lại bằng máy tính)

Tính đúng đắn

Việc chứng minh thuật toán này cũng đơn giản. Ta biểu diễn thuật toán này dưới dạng dãy truy hồi

{U_0} = a;\\ {U_n} = \frac{1}{2}\left( {{U_{n - 1}} + \frac{x}{{{U_{n - 1}}}}} \right);

Giả sử dãy có giới hạn hữu han, gọi giới nó là L. Ta cho qua giới hạn hai vế của biểu thức, ta được

L = \frac{1}{2}\left( L + \frac{x}{L} \right)

bằng biến đổi tương đương ta có được L^2 = x (Trên thực tế việc chứng minh dãy này hữu hạn và tiến đến L cũng không khó)

Tác giả của thuật Toán

Tác giả của thuật toán được cho là Hero of Alexandria sống ở thế kỉ thứ nhất sau công nguyên. Thông tin thêm về ông có thể xem tại đây. Có thể bạn đã biết ông qua công thức tính diện tích tam giác qua đồ dài ba cạnh của tam giác – công thức Heron.

Bạn đã thử thuật toán này với ví dụ nào chưa? Và tới đây bạn có tiếp tục sử dụng nút căn bậc hai trên máy tính không? 😀 😀 :v

Đăng bởi huwng

Đã đăng

Một suy nghĩ 9 thoughts on “Tính căn bậc hai của một số như thế nào?”

  2. Với sai số càng bé tầm 10^-9 thì thuật toán này đpt của nó là bao nhiêu nhỉ?
    Thực ra xưa nay tớ vẫn dùng binary search để tìm căn, đpt là O(Log2K) =)) sai số càng bé thì K càng lớn.

    Đã thích bởi 1 người

    Trả lời

    1. Ừa tớ cũng có nghĩ đến độ phức tạp rồi nhưng mà viết vội nên chưa có. Tớ sẽ tìm hiểu và bổ sung sau 😀
      Cảm ơn cậu nhé 😀

      Thích

      Trả lời
  3. Pingback: Tính căn bậc hai của một số như thế nào? — Hưng Nguyễn | vinhdu

Bình luận về bài viết này